IOU相关知识

IoU 作为目标检测算法性能 mAP 计算的一个非常重要的函数。

1. 什么是IOU

IoU 的全称为交并比（Intersection over Union），通过这个名称我们大概可以猜到 IoU 的计算方法。IoU 计算的是 “预测的边框” 和 “真实的边框” 的交集和并集的比值。

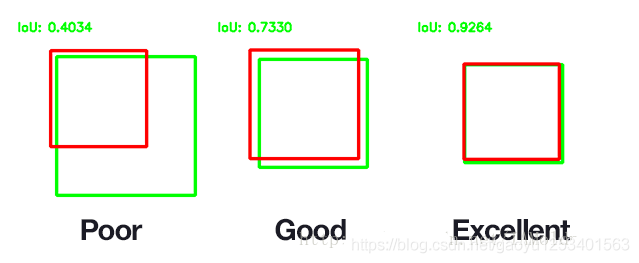
一般约定，在计算机检测任务中，如果IoU≥0.5，就说检测正确。当然0.5只是约定阈值，你可以将IoU的阈值定的更高。IoU越高，边界框越精确。

举例如下：绿色框是准确值，红色框是预测值。

2. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def calculateIoU(candidateBound, groundTruthBound):
    cx1 = candidateBound[0]
    cy1 = candidateBound[1]
    cx2 = candidateBound[2]
    cy2 = candidateBound[3]
 
    gx1 = groundTruthBound[0]
    gy1 = groundTruthBound[1]
    gx2 = groundTruthBound[2]
    gy2 = groundTruthBound[3]
 
    carea = (cx2 - cx1) * (cy2 - cy1) #C的面积
    garea = (gx2 - gx1) * (gy2 - gy1) #G的面积
 
    x1 = max(cx1, gx1)
    y1 = max(cy1, gy1)
    x2 = min(cx2, gx2)
    y2 = min(cy2, gy2)
    w = max(0, abs(x2 - x1))
    h = max(0, abs(y2 - y1))
    area = w * h #C∩G的面积
 
    iou = area / (carea + garea - area)
 
    return iou

3. 原理解析

计算两个图片的交集，首先想到的是考虑两个图片边框的相对位置，然后按照它们的相对位置分情况讨论。

相对位置无非以下几种：

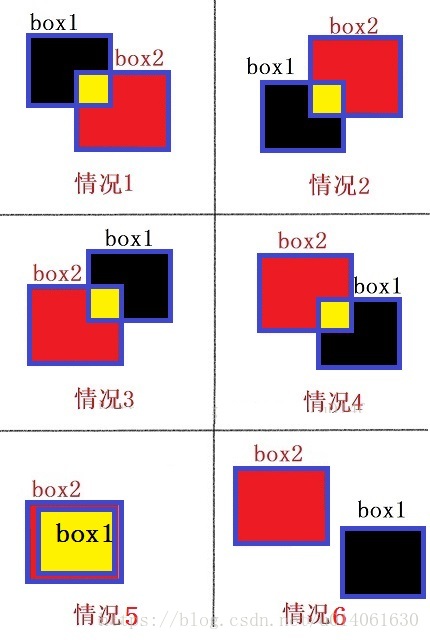
左上 左下 右上 右下 包含 互不相交

如下图所示：

但在实际上这样写代码是做不到的。

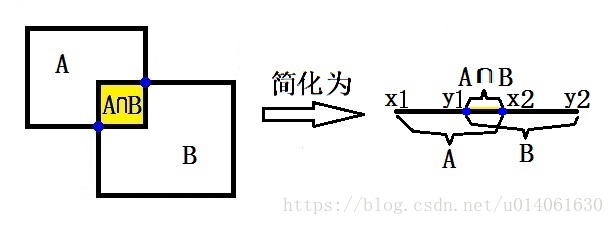
换个角度思考：两个框交集的计算的实质是两个集合交集的计算，因此我们可以将两个框的交集的计算简化为：

通过简化，我们可以清晰地看到，交集计算的关键是交集上下界点（图中蓝点）的计算。

我们假设集合 A 为 [x 1 x_{1}x1，x 2 x_{2}x2]，集合 B 为 [y 1 y_{1}y1，y 2 y_{2}y2]。然后我们来求AB交集的上下界限。

交集计算的逻辑

  • 交集下界 z 1 z_{1}z1：max ( x 1 , y 1 ) \text{max}(x_{1}, y_{1})max(x1,y1)
  • 交集上界 z 2 z_{2}z2：min ( x 2 , y 2 ) \text{min}(x_{2}, y_{2})min(x2,y2)
  • 如果 z 2 − z 1 z_{2}-z_{1}z2−z1 小于0，则说明集合 A 和集合 B 没有交集。

在YOLOv5的项目代码中，作者使用如下代码计算iou。

代码路径为：/yolov5-master/build/lib.win-amd64-3.9/utils/metrics.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def bbox_iou(box1, box2, x1y1x2y2=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2

    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    if CIoU or DIoU or GIoU:
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
        if CIoU or DIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            c2 = cw ** 2 + ch ** 2 + eps  # convex diagonal squared
            rho2 = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 +
                    (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4  # center distance squared
            if CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha = v / (v - iou + (1 + eps))
                return iou - (rho2 / c2 + v * alpha)  # CIoU
            return iou - rho2 / c2  # DIoU
        c_area = cw * ch + eps  # convex area
        return iou - (c_area - union) / c_area  # GIoU https://arxiv.org/pdf/1902.09630.pdf
    return iou  # IoU