Deep_Learning学习笔记2

极简手写数字识别模型

基础模型：神经网络

  • 套用房价预测的模型
  • 输入：由28*28改为784/每个像素值
  • 输出：1，预测的数据值

以类的方式组建网络

  • 初始化函数：定义每层的函数
  • Forward函数：层之间的串联方式
1
2
3
4
5
6
7
8
9
10
11
12
# 定义mnist数据识别网络结构，同房价预测网络
class MNIST(fluid.dygraph.Layer):
    def __init__(self, name_scope):
        super(MNIST, self).__init__(name_scope)
        name_scope = self.full_name()
        # 定义一层全连接层，输出维度是1,激活函数为None，即不使用激活函数
        self.fc = Linear(input_dim=784, output_dim=1, act=None)

    # 定义网络结构的前向计算过程
    def forward(self, inputs):
        outputs = self.fc(inputs)
        return outputs

input_dim设置为784,即输入为784

output_dim为1，即网络层数为1

act为None，即不使用激活函数

在init()中申明网络结构，在forward()函数中把这些结构串联，

训练过程

  • 代码几乎与房价预测任务一致

  • 包含四个部分：

    • 生成模型实例，设为“训练”状态
    • 配置优化器，SGD Optimizer
    • 两层循环的训练过程
    • 保存模型参数，便于后续使用

  • 仅在向模型灌入数据的代码不同

    • 先转变成np.array格式
    • 再转换成框架内置格式 to variable
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 通过with语句创建一个dygraph运行的context
# 动态图下的一些操作需要在guard下进行
with fluid.dygraph.guard():
    model = MNIST("mnist")
    # 启动训练模式
    model.train()
    # 加载训练集 batch_size 设为 16
    train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=16)
    # 定义优化器，使用随机梯度下降SGD优化器，学习率设置为0.001
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001,parameter_list=model.parameters())
    EPOCH_NUM = 10
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            # 准备数据并转化成符合框架要求的格式
            image_data = np.array([x[0] for x in data]). astype('float32')
            label_data = np.array([x[1] for x in data]). astype('float32').reshape(-1, 1)
            # 将格式转为飞桨动态图格式
            image = fluid.dygraph.to_variable(image_data)
            label = fluid.dygraph.to_variable(label_data)
            # 前向计算的过程
            predict = model(image)
            # 计算损失
            loss = fluid.layers.square_error_cost(predict, label)
            avg_loss = fluid.layers.mean(loss)
            # 每训练了1000批次的数据，打印下当前Loss的情况
            if batch_id != 0 and batch_id % 1000 == 0:
                print("epoch_id: {}, batch_id: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            # 后向传播，更新参数的过程
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()
# 保存模型
fluid.save_dygraph(model.state_dict(),'mnist1')

每训练1000批次打印的Loss数据如下:

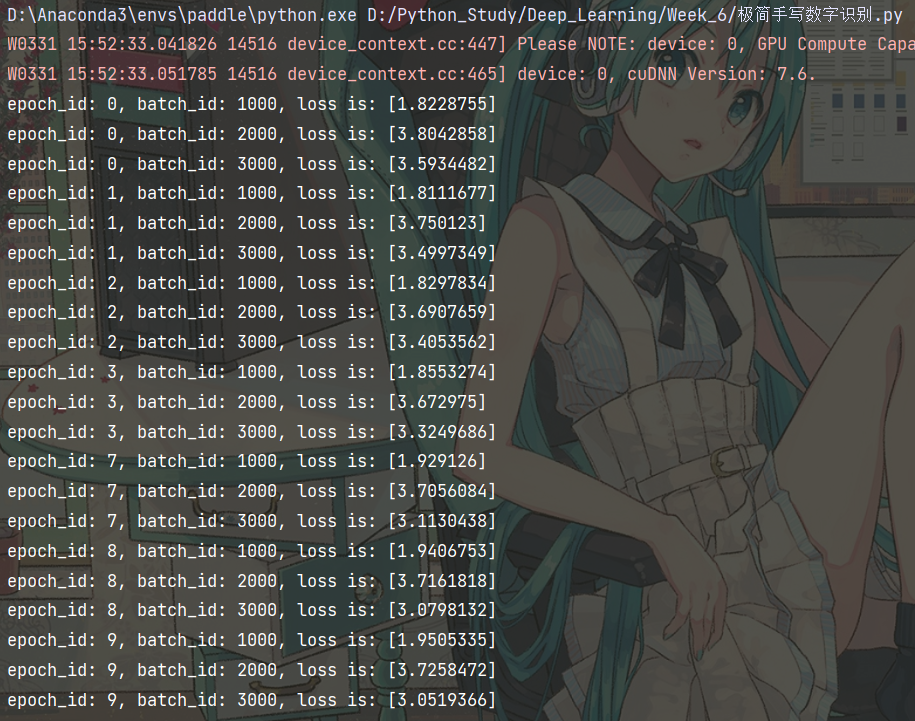
可以看出训练的效果并不好

  • Loss的值并没有在1以下，甚至有的还超过3
  • 从epoch0到epoch9，Loss值总体上下降趋势并不明显

测试效果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 测试效果
def load_image(img_path):
    im = Image.open(img_path).convert('L')
    # print(np.array(im))
    im = im.resize((28, 28), Image.ANTIALIAS)
    im = np.array(im).reshape(1, -1).astype(np.float32)
    im = 2 - im / 127.5
    return im

# 定义预测过程
with fluid.dygraph.guard():
    model = MNIST("mnist")
    params_file_path = 'mnist3'
    img_path = './work/example_0.jpg'
    # 加载数据模型
    model_dict, _ = fluid.load_dygraph("mnist3")
    model.load_dict(model_dict)

    model.eval()
    tensor_img = load_image(img_path)
    result = model(fluid.dygraph.to_variable(tensor_img))
    # 预测输出取整，即为预测的数字
    print("本次预测的数字是:",result.numpy().astype('int32'))

预测的结果如下图所示:

显然是不准确的

优化版手写数字识别模型

网络模型

多层感知机

  • 代码如下：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    # 定义多层全连接神经网络
    class MNIST(paddle.nn.Layer):
        def __init__(self):
            super(MNIST, self).__init__()
            # 定义两层全连接隐含层，输出维度是10，当前设定隐含节点数为10，可根据任务调整
            self.fc1 = Linear(in_features=784, out_features=10)
            self.fc2 = Linear(in_features=10, out_features=10)
            # 定义一层全连接输出层，输出维度是1
            self.fc3 = Linear(in_features=10, out_features=1)
        # 定义网络的前向计算，隐含层激活函数为sigmoid，输出层不使用激活函数
        def forward(self, inputs):
            # inputs = paddle.reshape(inputs, [inputs.shape[0], 784])
            outputs1 = self.fc1(inputs)
            outputs1 = F.sigmoid(outputs1)
            outputs2 = self.fc2(outputs1)
            outputs2 = F.sigmoid(outputs2)
            outputs_final = self.fc3(outputs2)
            return outputs_final
    • 输入层的尺度为28×28，但批次计算的时候会统一加1个维度（大小为batch size）。
    • 中间的两个隐含层为10×10的结构，激活函数使用常见的Sigmoid函数。
    • 与房价预测模型一样，模型的输出是回归一个数字，输出层的尺寸设置成1。

  • 训练效果

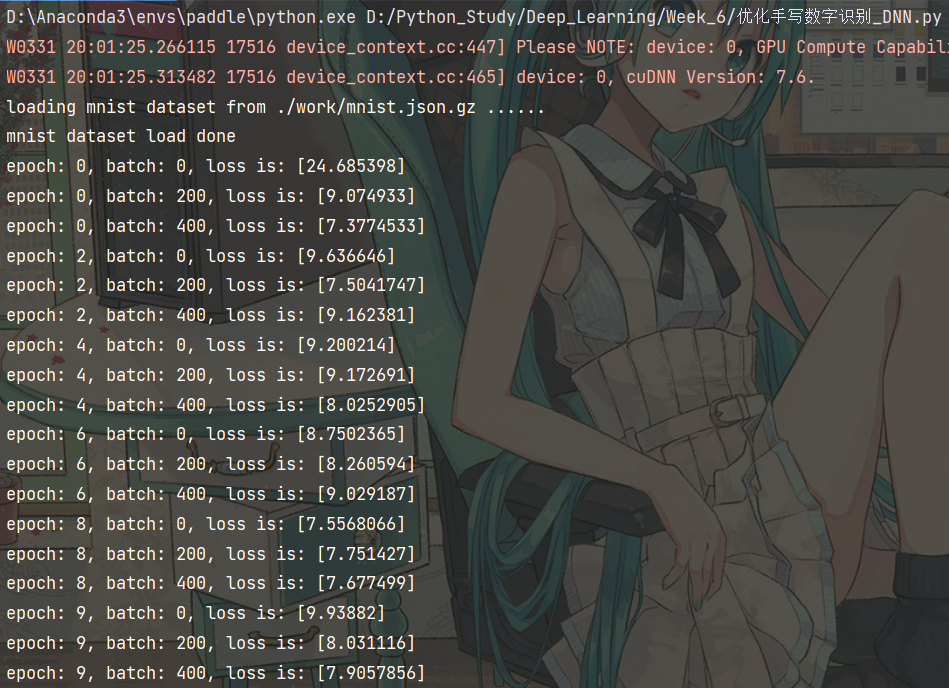
卷积神经网络

  • 代码如下

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    # 多层卷积神经网络实现
    class MNIST(paddle.nn.Layer):
        def __init__(self):
            super(MNIST, self).__init__()
            # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
            self.conv1 = Conv2D(in_channels=1, out_channels=20, kernel_size=5, stride=1, padding=2)
            # 定义池化层，池化核的大小kernel_size为2，池化步长为2
            self.max_pool1 = MaxPool2D(kernel_size=2, stride=2)
            # 定义卷积层，输出特征通道out_channels设置为20，卷积核的大小kernel_size为5，卷积步长stride=1，padding=2
            self.conv2 = Conv2D(in_channels=20, out_channels=20, kernel_size=5, stride=1, padding=2)
            # 定义池化层，池化核的大小kernel_size为2，池化步长为2
            self.max_pool2 = MaxPool2D(kernel_size=2, stride=2)
            # 定义一层全连接层，输出维度是1
            self.fc = Linear(input_dim=980, output_dim=1)
        # 定义网络前向计算过程，卷积后紧接着使用池化层，最后使用全连接层计算最终输出
        # 卷积层激活函数使用Relu，全连接层不使用激活函数
        def forward(self, inputs):
            x = self.conv1(inputs)
            x = F.relu(x)
            x = self.max_pool1(x)
            x = self.conv2(x)
            x = F.relu(x)
            x = self.max_pool2(x)
            x = paddle.reshape(x, [x.shape[0], -1])
            x = self.fc(x)
            return x

  • 训练结果如下

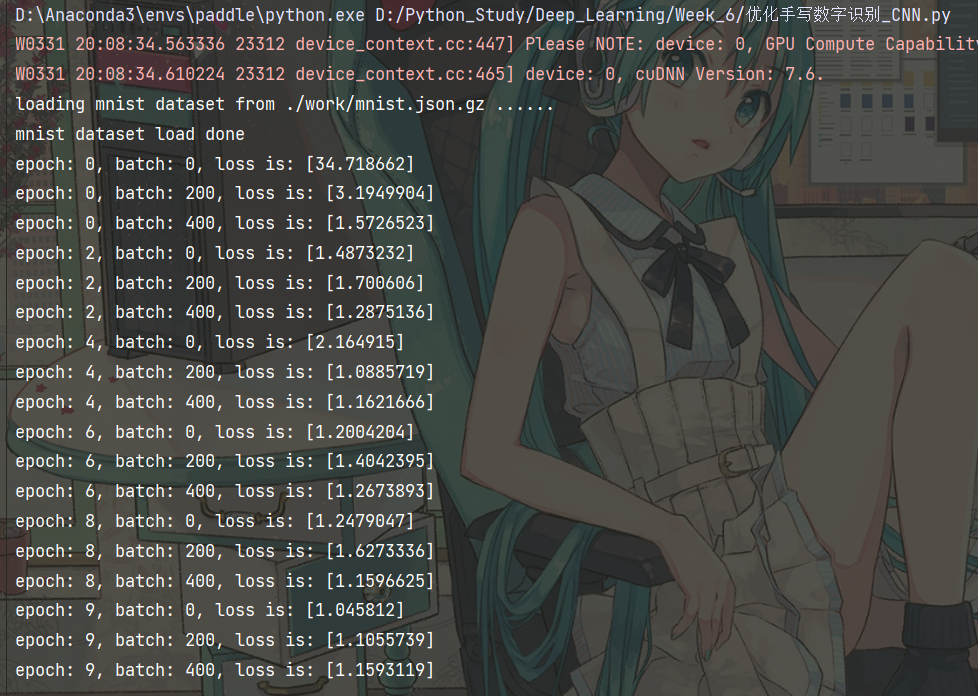
比较经典全连接神经网络和卷积神经网络的损失变化，可以发现卷积神经网络的损失值下降更快，且最终的损失值更小。

损失函数

均方误差

上述卷积神经网络的模型的损失函数用的即为均方误差。

交叉熵——sigmoid()

修改计算损失的函数:

  • 从：loss = paddle.nn.functional.square_error_cost(predict, label)
  • 到：loss = paddle.nn.functional.cross_entropy(predict, label)

训练结果如下：

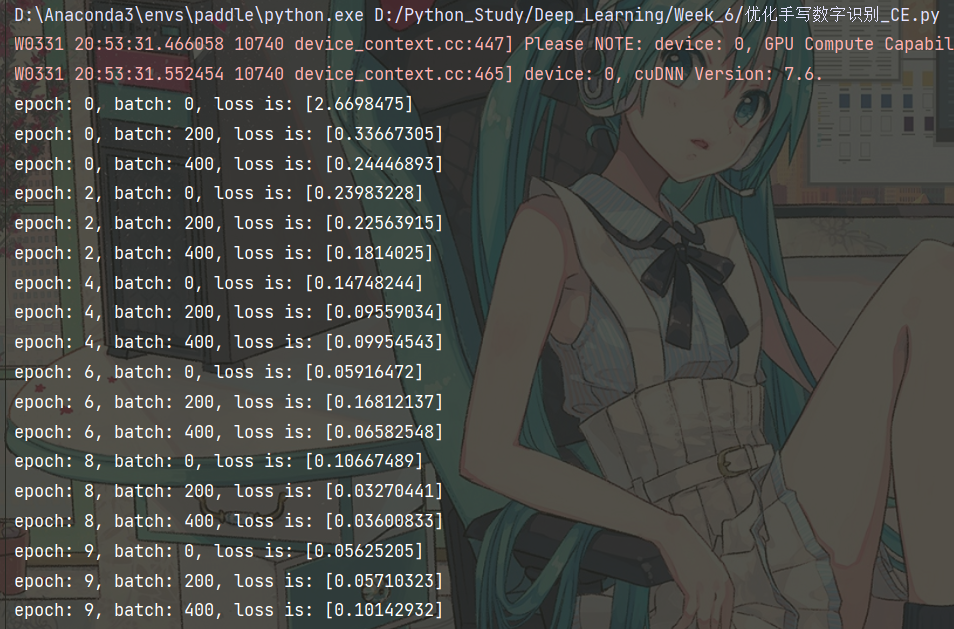
优化算法

在深度学习神经网络模型中，通常使用标准的随机梯度下降算法更新参数，学习率代表参数更新幅度的大小，即步长。当学习率最优时，模型的有效容量最大，最终能达到的效果最好。学习率和深度学习任务类型有关，合适的学习率往往需要大量的实验和调参经验。探索学习率最优值时需要注意如下两点：

  • 学习率不是越小越好。学习率越小，损失函数的变化速度越慢，意味着我们需要花费更长的时间进行收敛，如 图2 左图所示。
  • 学习率不是越大越好。只根据总样本集中的一个批次计算梯度，抽样误差会导致计算出的梯度不是全局最优的方向，且存在波动。在接近最优解时，过大的学习率会导致参数在最优解附近震荡，损失难以收敛，如 图2 右图所示。

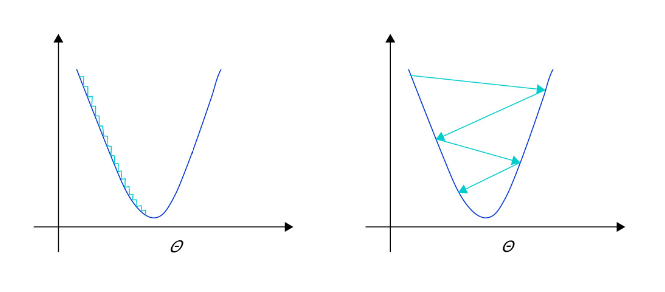
设置学习率

在训练前，我们往往不清楚一个特定问题设置成怎样的学习率是合理的，因此在训练时可以尝试调小或调大，通过观察Loss下降的情况判断合理的学习率，设置学习率的代码如下所示。

1
2
3
4
#设置不同初始学习率
opt = paddle.optimizer.SGD(learning_rate=0.001, parameters=model.parameters())
# opt = paddle.optimizer.SGD(learning_rate=0.0001, parameters=model.parameters())
# opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())

学习率的主流优化算法

学习率是优化器的一个参数，调整学习率看似是一件非常麻烦的事情，需要不断的调整步长，观察训练时间和Loss的变化。经过研究员的不断的实验，当前已经形成了四种比较成熟的优化算法：SGD、Momentum、AdaGrad和Adam，效果如下图所示。

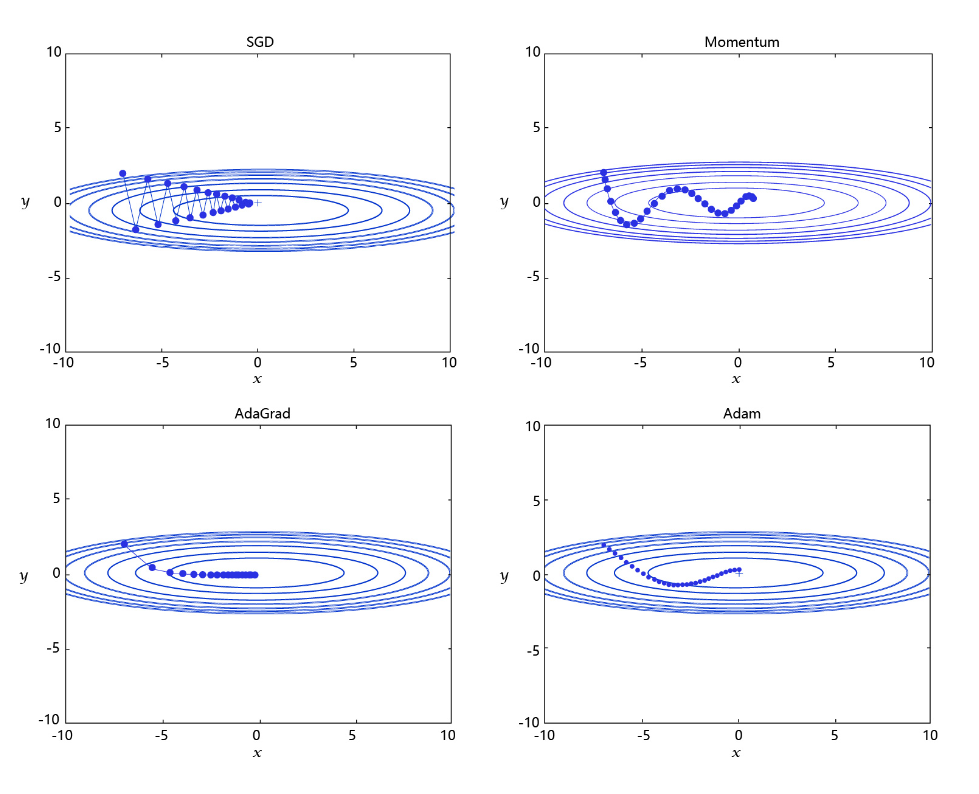
  • SGD： 随机梯度下降算法，每次训练少量数据，抽样偏差导致的参数收敛过程中震荡。
  • Momentum： 引入物理“动量”的概念，累积速度，减少震荡，使参数更新的方向更稳定。

每个批次的数据含有抽样误差，导致梯度更新的方向波动较大。如果我们引入物理动量的概念，给梯度下降的过程加入一定的“惯性”累积，就可以减少更新路径上的震荡，即每次更新的梯度由“历史多次梯度的累积方向”和“当次梯度”加权相加得到。历史多次梯度的累积方向往往是从全局视角更正确的方向，这与“惯性”的物理概念很像，也是为何其起名为“Momentum”的原因。类似不同品牌和材质的篮球有一定的重量差别，街头篮球队中的投手（擅长中远距离投篮）喜欢稍重篮球的比例较高。一个很重要的原因是，重的篮球惯性大，更不容易受到手势的小幅变形或风吹的影响。

  • AdaGrad： 根据不同参数距离最优解的远近，动态调整学习率。学习率逐渐下降，依据各参数变化大小调整学习率。

通过调整学习率的实验可以发现：当某个参数的现值距离最优解较远时（表现为梯度的绝对值较大），我们期望参数更新的步长大一些，以便更快收敛到最优解。当某个参数的现值距离最优解较近时（表现为梯度的绝对值较小），我们期望参数的更新步长小一些，以便更精细的逼近最优解。类似于打高尔夫球，专业运动员第一杆开球时，通常会大力打一个远球，让球尽量落在洞口附近。当第二杆面对离洞口较近的球时，他会更轻柔而细致的推杆，避免将球打飞。与此类似，参数更新的步长应该随着优化过程逐渐减少，减少的程度与当前梯度的大小有关。根据这个思想编写的优化算法称为“AdaGrad”，Ada是Adaptive的缩写，表示“适应环境而变化”的意思。RMSProp是在AdaGrad基础上的改进，学习率随着梯度变化而适应，解决AdaGrad学习率急剧下降的问题。

  • Adam： 由于动量和自适应学习率两个优化思路是正交的，因此可以将两个思路结合起来，这就是当前广泛应用的算法。

利用不同的优化算法训练模型

1
2
3
4
5
#四种优化算法的设置方案，可以逐一尝试效果
    opt = paddle.optimizer.SGD(learning_rate=0.01, parameters=model.parameters())
    # opt = paddle.optimizer.Momentum(learning_rate=0.01, momentum=0.9, parameters=model.parameters())
    # opt = paddle.optimizer.Adagrad(learning_rate=0.01, parameters=model.parameters())
    # opt = paddle.optimizer.Adam(learning_rate=0.01, parameters=model.parameters())

超参数

在深度学习中，超参数有很多，比如学习率α、使用momentum或Adam优化算法的参数（β1，β2，ε）、层数layers、不同层隐藏单元数hidden units、学习率衰退、mini=batch的大小等。