简介

topsis综合评价法即根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价，是一种逼近于理想解的排序法。

基本过程为先将原始数据矩阵统一指标类型（一般正向化处理）得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

适用于：决策层中指标的数据是已知的，利用这些数据使得评价的更加准确。

算法原理

统一指标类型

将所有的指标转化为极大型称为指标正向化(最常用)

第一步：将原始矩阵正向化

常见的四种指标：

指标名称 指标特点 例子
极大型(效益型)指标 越大(多)越好 成绩、GDP增速、企业利润
极小型(成本型)指标 越小(少)越好 费用、坏品率、污染程度
中间型指标 越接近某个值越好 水质量评估时的PH值
区间型指标 落在某个区间最好 体温、水中植物性营养物量

注：将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标
转换的函数形式可以不唯一

各种类型指标的转换

  • 极小型指标→极大型指标

    • 公式：$max-x$

    • 补充：如果所有元素均为正数，那么也可以使用1/x

  • 中间型指标→极大型指标

    • 中间型指标：指标值既不要太大也不要太小，取某特定值最好(如水质量评估PH值)。

    • 公式：$M=max{|X_i-X_{best}|}$,$\widetilde{X_i}=1-\frac{|X_i-X_{best}|}{M}$，其中{Xi}是一组中间型指标序列，且最佳的数值为Xbest。

  • 区间型指标→极大型指标

    • 区间型指标：指标值落在某个区间内最好，例如人的体温在36°～37°这个区间比较好。

    • 公式：$M=max[{a-min({x_i}),max(x_i)-b}]$， $\widetilde{X_i}=\begin{cases}{ 1-\frac{a-x_i}{M},x_i<a} \ 1 , a\le x_i \le b\ 1-\frac{x_i-b}{M}, x_i > b \end{cases}$

      其中$x_i$是一组区间型指标序列，且最佳的区间为[a,b]

第二步：正向化矩阵标准化

标准化的目的是消除不同指标量纲的影响

第三步：计算得分并归一化

例题

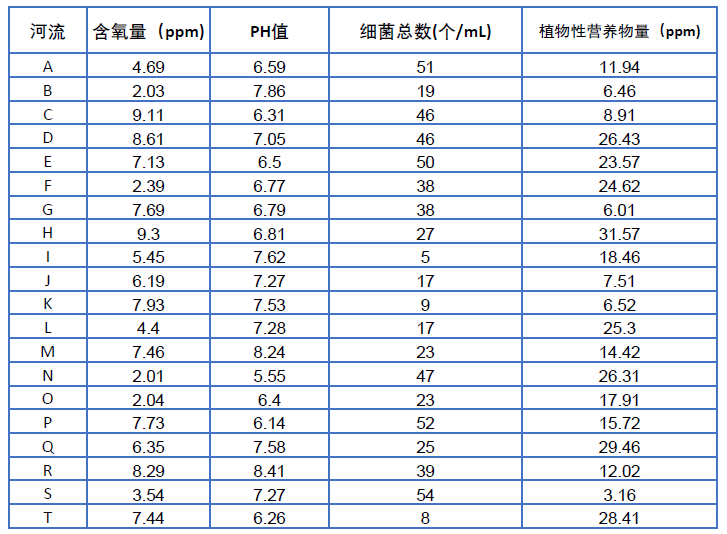
题目：评价下表中20条河流的水质情况。
注：含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10‐20之间最佳，超过20或低于10均不好。

实现代码

第一步：把数据复制到工作区，并将矩阵命名为X

（1）在工作区右键，点击新建（Ctrl+N)，输入变量名称为X
（2）在Excel中复制数据，再回到Excel中右键，点击粘贴Excel数据（Ctrl+Shift+V）
（3）关掉这个窗口，点击X变量，右键另存为，保存为mat文件
注意：代码和数据要放在同一个目录下，且Matlab的当前文件夹也要是这个目录。

==导入数据代码：==

1
load XX.mat

第二步：判断是否需要正向化

1
[n,m] = size(X); %将表格数据转换为矩阵

==正向化代码：==

  • 极小型→极大型

    1
    2
    3
    4
    function [posit_x] = Min2Max(x)
        posit_x = max(x) - x;
         %posit_x = 1 ./ x;    %如果x全部都大于0，也可以这样正向化
    end

  • 中间型→极大型

    1
    2
    3
    4
    function [posit_x] = Mid2Max(x,best)
        M = max(abs(x-best));
        posit_x = 1 - abs(x-best) / M;
    end

  • 区间型→极大型

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    function [posit_x] = Inter2Max(x,a,b)
        r_x = size(x,1);  % row of x 
        M = max([a-min(x),max(x)-b]);
        posit_x = zeros(r_x,1);   %zeros函数用法: zeros(3)  zeros(3,1)  ones(3)
        % 初始化posit_x全为0  初始化的目的是节省处理时间
        for i = 1: r_x
            if x(i) < a
               posit_x(i) = 1-(a-x(i))/M;
            elseif x(i) > b
               posit_x(i) = 1-(x(i)-b)/M;
            else
               posit_x(i) = 1;
            end
        end
    end

第三步：对正向化后的矩阵进行标准化

1
2
3
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)

第四步：计算与最大值的距离和最小值的距离，并算出得分

1
2
3
4
5
6
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5;   % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N);    % 未归一化的得分
disp('最后的得分为：')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')

补充——幻方矩阵

A = magic(5) % 幻方矩阵
M = magic(n)返回由1到n^2的整数构成并且总行数和总列数相等的n×n矩阵。阶次n必须为大于或等于3的标量。
sort(A)若A是向量不管是列还是行向量，默认都是对A进行升序排列。sort(A)是默认的升序，而sort(A,’descend’)是降序排序。
sort(A)若A是矩阵，默认对A的各列进行升序排列
sort(A,dim)
dim=1时等效sort(A)
dim=2时表示对A中的各行元素升序排列
A = [2,1,3,8]
Matlab中给一维向量排序是使用sort函数：sort（A），排序是按升序进行的，其中A为待排序的向量；
若欲保留排列前的索引，则可用 [sA,index] = sort(A,’descend’) ，排序后，sA是排序好的向量，index是向量sA中对A的索引。
sA = 8 3 2 1
index = 4 3 1 2