数学建模综述
数学建模基本题型
预测类
概述
指的是通过分析已有的数据或者现象,找出其内在发展规律,然后对未来情形做出预测的过程。
根据已知条件和求解目的,往往将预测类问题分为:
- 小样本内部预测
- 大样本内部预测
- 小样本未来预测
- 大样本随机因素或周期特征的未来预测
- 大样本的未来预测
例题——2021年第十一届MathorCup高校数学建模挑战赛B题
B题 三维团簇的能量预测
团簇,也称超细小簇,属纳米材料的尺度概念。团簇是由几个乃至上
千个原子、分子或离子通过物理或化学结合力组成的相对稳定的微观或亚
微观聚集体,其物理和化学性质随所含的原子数目而变化。团簇是材料尺度纳米材料的一个概念。团簇的空间尺度是几埃至几百埃的范围,用无机分子来描述显得太小,用小块固体描述又显得太大,许多性质既不同于单个原子分子,又不同于固体和液体,也不能用两者性质的简单线性外延或内插得到。因此,人们把团簇看成是介于原子、分子与宏观固体物质之间的物质结构的新层次。团簇科学是凝聚态物理领域中非常重要的研究方向。
团簇可以分为金属团簇和非金属团簇,由于金属团簇具有良好的催化性能,因此备受关注。但由于团簇的势能面过于复杂,同时有时候还需要考虑相对论效应等,所以搜索团簇的全局最优结构(即能量最低)显得尤为困难。其中,传统的理论计算方法需要数值迭代求解薛定谔方程,并且随原子数增加,高精度的理论计算时间呈现指数增长,非常耗时。因此,目前需要对这种方法加以改进,例如:考虑全局优化算法,结合机器学习等方法,训练团簇结构和能量的关系,从而预测新型团簇的全局最优结构,有利于发现新型团簇材料的结构和性能。请建立三维团簇能量预测的数学模型,并使用附件中的坐标和能量数据,解决下列问题。
备注:附件中数据集格式为xyz,第一行是原子数,第二行是能量,后面是原子的三维坐标。可用文本阅读器打开,并用VMD 等软件进行可视化。
问题1:针对金属团簇,附件给出了1000 个金团簇$Au_{20}$的结构,请你们建立金团簇能量预测的数学模型,并预测金团簇$Au_{20}$ 的全局最优结构,
描述形状;
问题2:在问题1 的基础上,请你们设计算法,产生金团簇不同结构的异构体,自动搜索和预测金团簇$Au_{32}$的全局最优结构,并描述其几何形
状,分析稳定性;
问题3:针对非金属团簇,附件给出了3751 个硼团簇$B_{45}$的结构,请你们建立硼团簇能量预测的数学模型,并预测硼团簇B45的全局最优结构,描述形状;
问题4:在问题3 的基础上,请你们设计算法,产生硼团簇不同结构的异构体,自动搜索和预测硼团簇$B_{40}$的全局最优结构,并描述其几何形状,分析稳定性。
注:预测问题主要是以某个小问的形式出现,很少有整个赛题所有小问全是预测要求的
评价类
指的是按照一定的标准对事物的发展或者现状进行划分的过程在数学建模中题点可体现在对生态环境,社会建设,方案策略等进行评价。评价类赛题往往没有明确的指标体系和评价标准,往往是需要查阅各类资料进行构建的,因此评价类赛题也没有明确的答案。
注:解决评价类赛题的关键是指标体系的构建,构建完评价体系后在选择合适的评价方法即可,体系建立应秉承全面,准确,独立的三要素
机理分析类赛题
机理分析是根据对现实对象特性的认识,分析其因果关系,找出反映内部机理的规律。在求解机理分析类问题时首先需要探寻与问题相关的物理,化学,经济等相关的知识,然后通过对已知数据或现象的分析对事物的内在规律做出必要的假设,最后通过构建合适的方程或关系式对其内在规律进行数值表达。
注:机理分析立足于建立事物内部的规律,相对于其他类型的赛题均有章可循,机理分析类赛题往往需要结合众多关联知识才可以进行求解,如空气动力学,流体力学,热力学等
优化类
指在现有现有条件固定的情况下,如何使目标效果达到最佳。如在一座城市公交车公司拥有的公交车数量是固定的,问如何安排线路能够使盈利达到最高。优化类问题往往需要分析三个关键因素:目标函数,决策变量和约束条件,三者往往缺一不可。
注:解决优化类赛题必须知道优化的目的,约束的条件和所求解的关键变量,需要有较强的编程能力和赛题分析挖掘能力
数学建模算法
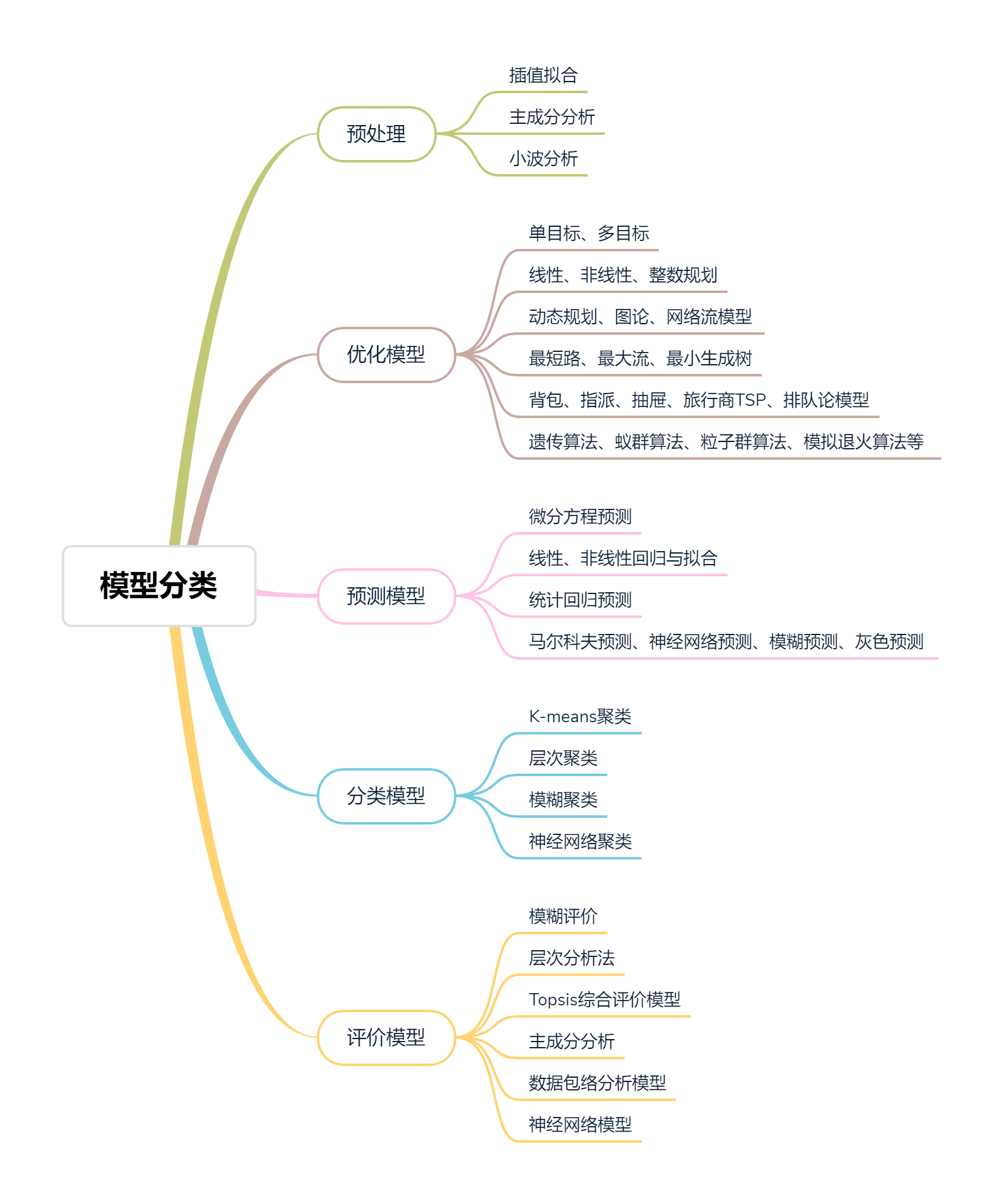
.jpg)