什么是Attention(注意力机制)

在认知科学中，由于信息处理的瓶颈，人类会选择性地关注所有信息的一部分，同时忽略其他可见的信息。通俗点来说就是，我们在认知事物时，有着明显的主观色彩和测重，比如「我喜欢踢足球，但我更喜欢打篮球」，对于人类显然知道这个人更喜欢打篮球，但对于深度学习或计算机来说，它没办法领会到「更」的含义，因此没有办法知道这个结果。所以我们在训练模型的时候，会大家「更」字的权重，让它在句子中的重要性获得更大的占比。

综上，注意力机制主要有两个方面：决定需要关注输入的哪部分；分配有限的信息处理资源给重要的部分。

什么是Self-Attention

在知道了attention在机器学习中的含义之后（下文都称之为注意力机制）。人为设计的注意力机制，是非常主观的，而且没有一个准则来评定，这个权重设置为多少才好。所以，如何让模型自己对变量的权重进行自赋值成了一个问题，这个权重自赋值的过程也就是self-attention。

Self-Attention原理

$$
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V
$$

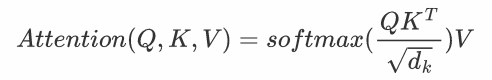
Softmax操作

抛开Q,K,V三个矩阵不谈，self-attention最原始的形态是$Softmax(XX^T)X$

这个公式表示什么意思呢？

==Q1：$XX^T$代表什么？==

一个矩阵乘以它自己的转置，会得到什么结果，有什么意义？

我们知道，矩阵可以看作由一些向量组成，一个矩阵乘以它自己转置的运算，其实可以看成这些向量分别与其他向量计算内积。（此时脑海里想起矩阵乘法的口诀，第一行乘以第一列、第一行乘以第二列……嗯哼，矩阵转置以后第一行不就是第一列吗？这是在计算第一个行向量与自己的内积，第一行乘以第二列是计算第一个行向量与第二个行向量的内积第一行乘以第三列是计算第一个行向量与第三个行向量的内积…..）

回想我们文章开头提出的问题，向量的内积，其几何意义是什么？

A1：表征两个向量的夹角，表征一个向量在另一个向量上的投影

实例：我们假设$X=[x^T_1;x^T_2;x^T_3]$，其中X为一个二维矩阵，$X^T_i$为一个行向量，下图中模拟运算了$XX^T$：

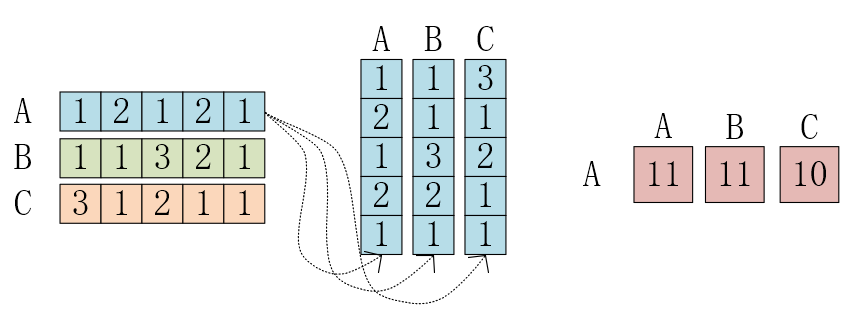
首先，行向量$X^T_i$分别与自己和其他两个向量做内积，得到了一个新的向量。

==Q2：新的向量有什么意义？表征什么？==

A2：投影的值大，说明两个向量相关度高。

更进一步，这个向量是词向量，是词在高维空间的数值映射。词向量之间相关度高表示什么？是不是在一定程度上（不是完全）表示，在关注词A的时候，应当给予词B更多的关注？

==Q3：$XX^T$的意义是什么？==

A3：矩阵$XX^T$是一个方阵，我们以行向量的角度理解，里面保存了每个向量与自己和其他向量进行内积运算的结果。

==Q4：Softmax操作的意义是什么？==

回到Softmax的公式：$Softmax(z_i)=\frac{e^{z_i}}{\sum^C_{c=1}e^{z_c}}$

A4：归一化。

也就是说通过Softmax操作后，这些数字的和为1了。

==Q5：那么Attention机制的核心是什么呢？==

A5：加权求和。

Q,K,V矩阵

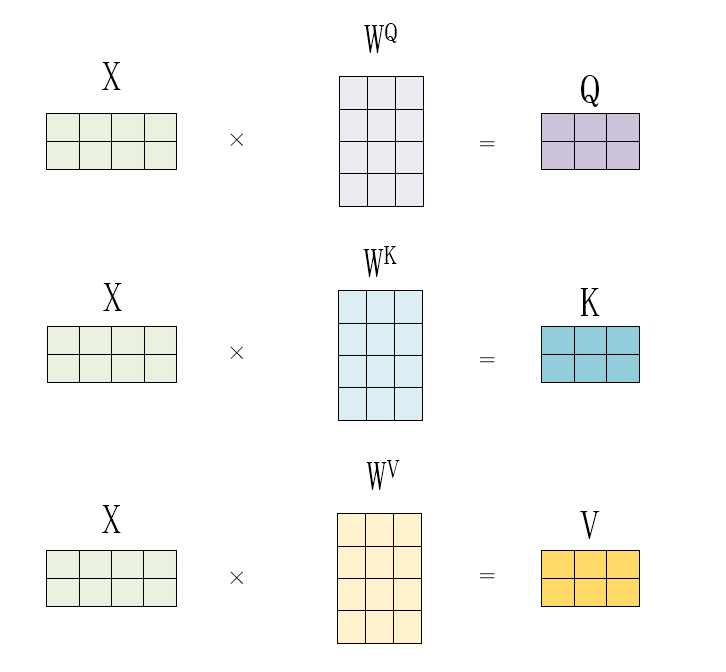
在很多文章中提到的Q,K,V矩阵、查询矩阵之类的字眼，本质上都是X矩阵的线性变换，其来源是X与某个矩阵的乘积。

==Q6：为什么不直接使用X而要对其进行线性变换呢？==

A6：当然是为了提升模型的拟合能力，矩阵W都是可以训练的，起到一个缓冲的作用。

$\sqrt{d_k}$的意义

假设Q,K里的元素全为0，方差为1，那么$A^T=Q^TK$中元素的均值为0，方差为d。当d变得很大时，A中的元素的方差也会变得很大，如果A中的元素方差很大，那么Softmax(A)的分布会趋于陡峭(分布的方差大，分布集中在绝对值大的区域)。

总结：Softmax(A)的分布会和d有关。因此A中每一个元素除以$\sqrt{d_k}$后，方差又变为1。这使得Softmax(A)的分布陡峭程度与d解耦，从而使得训练过程中梯度保持稳定。

对self-attention来说，它跟每一个input vector都做attention，所以没有考虑到input sequence的顺序。

Self-Attention的优点

与RNN相比，RNN的一个最大的问题是：前面的变量在经过多次RNN计算后，已经失去了原有的特征。越到后面，最前面的变量占比就越小，这是一个很反人类的设计。而self-attention在每次计算中都能保证每个输入变量a aa的初始占比是一样的，这样才能保证经过self-attention layer计算后他的注意力系数是可信的。

总结下来，它的优点是：

需要学习的参数量更少
可以并行计算
能够保证每个变量初始化占比是一样的

Multi-head Self-Attention

这里继续讲解multi-head self-attention，所谓head也就是指一个a aa衍生出几个q , k , v 。上述所讲解的self-attention是基于single-head的。以2 head为例：

首先，$a^i$先生成$q^1$，$ k^1$，$ v^1$。然后，接下来就和single-head不一样了，$q^i$生成 $q^{i,1}$,$q^{i,2}$，生成的方式有两种：

$q^i$乘上一个$W^{q,1}$得到 $q^{i,1}$，乘上 $W^{q,2}$得到$q^{i,2}$这个和single-head的生成是差不多的；
$q^i$**直接从通道维，平均拆分成两个，得到$ q^{i,1}$,$q^{i,2}$；

这两种方式，在最后结果上都差不多。至于为啥，后面会讲一下原因。

那么这里的图解使用第1个方式，先得到$q^{i,1}$ $k^{i,1}$ $v^{i,1}$。对 $a^j$做同样的操作得到 $q^{j,1}$**, $k^{j,1}$,$ v^{j,1}$。这边需要注意的一点，$q^{i,1}$是要和$k^{j,1}$做矩阵乘法，而非$k^{j,2}$，一一对应。后面计算就和single-head一样了，最后得到$b^{i,1}$。